 yükleniyor...
yükleniyor... | | |||||||
| Konu Kimliği: Konu Sahibi Medineweb,Açılış Tarihi: 03 Ağustos 2012 (21:58), Konuya Son Cevap : 03 Ağustos 2012 (22:07). Konuya 9 Mesaj yazıldı |
  |
| | LinkBack | Seçenekler | Değerlendirme |
| | Mesaj No:1 |
| Durumu: Medine No : 13301 Üyelik T.:
04 Şubat 2011 | DGS Geometri Dersi Konu Özetleri GEOMETRİK KAVRAMLAR Geometride Nokta,Doğru, Düzlem gibi kavramlar tanımsız olarak kabul edilir. 1. Nokta: biçiminde gösterilir. Boyutu yoktur. 2. Doğru: İki uçtan sınırsız noktalar kümesidir.  3. Düzlem: Her yönde sonsuza giden noktalar kümesidir. E düzlemi dört yönde de sonsuza kadar gider.  E düzlemi yandaki gibi gösterilir. 4. Doğru Parçası : İki nokta ile bu iki nokta arasında kalan noktaların birleşimidir. [AB] sembolüyle gösterilir. [AB] ® AB doğru parçası |AB| ® AB doğru parçasının uzunluğu 5. Işın : Bir başlangıç noktası olup sonsuza giden noktalar kümesidir. [AB ® AB ışını 6. Yarı Doğru: [AB ışınından A noktasının çıkarılması ile elde edilen kümeye AB yarıdoğrusu denir. ]AB sembolüyle gösterilir. Doğrusal nokta kümelerinin gösterimi  [AB]: A ve B noktaları dahil. [AB[: A noktası dahil, B noktası dahil değil ]AB[: A ve B noktaları dahil değil AÇILAR Başlangıç noktaları ortak iki ışının birleşimine açı denir. şekilde [AC ve [AB ışınının oluşturduğu açı BAC açısıdır. [ABÈ[AC = BAC açısıdır.BAC, CAB olarak veya A ile gösterilir.[AB ve [AC ışınları açının kenarları,  A noktası açının köşesidir. Açı yazılırken açının köşesi olan nokta ortada yazılır. 1. Açının Ölçüsü [AB ile [AC arasındaki açıklığın ifadesine açının ölçüsü denir. BAC açısının ölçüsü a dır.m(BAC) = a veya m(A) = a olarak gösterilir.  ölçüleri eşit olan açılara eş açılar denir. 2. Açının Düzlemde Ayırdığı Bölgeler Bir açı düzlemi üç bölgeye ayırır. a. Açının kendisi [AB ve [AC ışınları. b. İç bölge (taralı alan) c. Dış bölge  3. Açı ölçü birimleri Açı ölçüsü birimi olarak genelde derece kullanılır. Dereceden başka Grad ve Radyan birimleri de kullanılır. Açı ölçüsü birimleri arasında, 360° = 400 G(grad) = 2p (radyan) eşitliği vardır. Bir ışının başlangıç noktası etrafında bir tur döndürülmesi ile elde edilen açı 360° dir. Derecenin alt birimleri 1° = 60' (dakika) 1' = 60" (saniye) 1° = 3600" dir. 90° = 89° 59' 60" ve 180° = 179° 59' 60" olur.  4. Ölçülerine göre açılar a. Ölçüsü 0° ile 90° arasında olan açılara dar açı denir.  b. Ölçüsü 90° olanaçılara dik açı denir  c. Ölçüsü 90° ile 180°arasında olanaçılara geniş açı denir.  d. Ölçüsü 180° olanaçılara doğru açıdenir.  e. Ölçüsü 360° olan açıya tam açı denir.  5. Komşu açılar Köşeleri ve birer ışınları ortak olan, iç bölgesi ortak olmayan açılara komşu açılar denir. CAD ile DAB komşu açılardır.  6. Açıortay Açıyı iki eşit parçaya bölen ışına açıortay denir. [AD, CAB açısının açıortayıdır. Açıortay üzerinde alınan her noktanın açının kollarına olan dik uzaklıkları eşittir.  7. Tümler açı Ölçüleri toplamı 90° olan iki açıya tümler açılar denir. m(CAD)+m(DAB)=90° a+b=90° a açısının tümlerinin ölçüsü (90° � a) dır.  Komşu tümler iki açının açıortay doğruları arasındaki açının ülçüsü 45° dir.  [OA] ^ [OB] m(KOL) = 45° 8. Bütünler açı Ölçüleri toplamı 180° olan iki açıya bütünler açılar denir.  m(DAB)+m(CAD)=180° x+y=180° x açısının bütünlerinin ölçüsü (180° � x) dir. Komşu bütünler iki açının açıortay doğruları arasındaki açının ölçüsü 90° dir.  m(KOL) = 90° 9. Ters Açılar Kesişen iki doğrunun oluşturduğu açılardan komşu olmayanlara ters açılar denir. Ters açıların ölçüleri eşittir.  m(x)=m(z) ve m(t)=m(y) dir.  10. Paralel iki doğrunun bir kesenle yaptığı açılar a. Yöndeş açılar d1 // d2 ise  Yöndeş açıların ölçüleri eşittir.  m(a) = m(x) ; m(b) = m(y) m(c) = m(z) ; m(d) = m(t) b. İçters açılar d1 // d2 ise  a ile z ve b ile t içters açılarıdır. İçters açıların ölçüleri eşittir. m(a) = m(z); m(b) = m(t)  Dışters açılar d1 // d2 ise  Dışters açıların ölçüleri eşittir. m(c)=m(x)=m(d)=m(y)  d. Karşı durumlu açılar d1 // d2 ise  Karşı durumlu açıların toplamı 180° dır. m(a) + m(t) = 180°; m(b) + m(z) = 180°  Karşı durumlu açıların açıortayları arasındaki açının ölçüsü 90° dir. Paralel doğrular arasında birden fazla kesenin olduğu durumlarda kesişim noktalarından yeni paraleller çizilir. e. Birden fazla kesenli durumlar d1 // d2 ise B noktasındand1 ve d2 doğrularınaparalel çizersek m(ABC) = a + b olur.  B noktasından paralel çizersekm(ABD) + x = 180° m(DBC) + z = 180° buradan x + y + z = 360° dir.  f. Paralel doğrular arasındaki ardışık zıt yönlü açılar d1 // d2 ise a + b + c = x + y olur. Bu tür soruları kırılma noktalarından paraleller çizerek de çözebiliriz.  g. Kolları paralel ve kolları dik açılar Açıları oluşturan ışınlar aynı yönde ve paralel ise bu iki açının ölçüsü eşittir.  Açıları oluşturan ışınlar zıt yönlü ve paralel ise bu iki açının ölçüsü eşittir.  Açıları oluşturan ışınlardan biri aynı diğeri zıt yönlü ve paralel ise bu iki açının ölçüleri toplamı; a + b = 180° olur.  Kenarları birbirine dik karşılıklı iki açının ölçüleri toplamı a + b = 180° olur.  Kenarları şekildeki gibi birbirine dik açıların ölçüleri eşittir.  alıntı |
 |
 Konu Sahibi Medineweb 'in açmış olduğu son Konular Aşağıda Listelenmiştir
Konu Sahibi Medineweb 'in açmış olduğu son Konular Aşağıda Listelenmiştir
| |||||
| Konu | Forum | Son Mesaj Yazan | Cevaplar | Okunma | Son Mesaj Tarihi |
| | İlahiyat Öğrencileri İçin Genel Paylaşımlar | nurşen35 | 87 | 37931 | 23 Mayıs 2015 20:53 |
| | Videolar/Slaytlar | Kara Kartal | 3 | 4322 | 10 Mayıs 2015 15:16 |
| | İslami Haberler | Medineweb | 0 | 2897 | 10 Mayıs 2015 15:13 |
| | Ayın Üyesi | 9Esra | 13 | 9695 | 30 Nisan 2015 13:29 |
| | Tefsir Çalışmaları | Medineweb | 0 | 3556 | 19 Nisan 2015 14:45 |
| | Mesaj No:2 |
| Durumu: Medine No : 13301 Üyelik T.:
04 Şubat 2011 | Üçgenler Konu Özeti Bir doğru üzerinde olmayan (doğrusal olmayan) A,B,C gibi üç noktanın birleşiminden oluşan kapalı şekle ÜÇGEN denir.  Bir üçgen noktalar kümesidir ve içinde bulunduğu düzlemi üç ayrı noktalar kümesine ayırır. Bunlar; a)Üçgenin İçinde Kalan Noktalar Kümesi b)Üçgenin Kendisi c)Üçgenin Dışında Kalan Noktalar Kümesi  Bir Üçgenin Temel Elemanları 1.Üçgenin Kenarları:[BC],[AC],[AB] doğru parçalarına “Üçgenin Kenarları” denir. Kenar uzunlukları karşılarındaki açıların kenarlarıyla adlandırılırlar. 2.Üçgenin İç Açıları:Üçgenin iki kenarının oluşturduğu her bir açı “Üçgenin İç Açısı” olarak adlandırılır. Bir üçgenin iç açıları toplamı 180º`dir. 3.Üçgenin Dış Açıları:Üçgenin iç açılarının komşu bütünleri olan açılara “Üçgenin Dış Açıları” denir. Bir dış açı kendisine komşu olmayan iki iç açının toplamına eşittir. Bir üçgenin iç açısıyla dış açısının toplamı 180º`dir. Bir üçgenin dış açıları toplamı ise 360º`dir.  Bir Üçgenin Yardımcı Elemanları 1.Üçgenin Yüksekliği:Üçgenin bir köşesinden karşı tarafa indirilen, köşe ile kenar arasında kalan doğru parçasına “Üçgenin Yüksekliği” denir.”H” ile gösterilir.  2.Üçgenin Kenar Ortayları:Üçgenin bir köşe ile bu köşenin karşısındaki kenarın orta noktasını birleştiren doğru parçasına “Üçgenin Kenar Ortayı” denir. “V” ile gösterilir.  3.Üçgenin Açı Ortayı:Üçgenin açılarını iki eş açıya bölen doğruların,köşe ile kenar arasında kalan doğru parçasına “ÜÇGENİN AÇI ORTAYI” denir. ” N” ile gösterilir.  Üçgenin Kenarları Arasındaki Bağıntılar Bir üçgende iki kenarın uzunlukları toplamı üçüncü kenar uzunluğundan büyük;iki kenar uzunluğunun farkı, üçüncü kenarı uzunluğunda küçüktür. Üçgenin Açıları Arasındaki Bağıntılar Bir üçgende, bir köşedeki iç açı ile dış açının toplamı 180º`dir.Bir üçgende, bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir. Üçgenin Kenar Uzunluklar ve Açıları Arasındaki Bağıntılar Bir üçgende ölçüsü büyük olan kenar karşısında büyük açı, küçük olan kenar karşısında küçük kenar vardır. Üçgenin Çeşitleri 1.Kenarlarına Göre Üçgenler a)Çeşit Kenar Üçgen:Üçgenin kenarlarının hepsi farklıysa bu üçgene “Çeşit Kenar Üçgen” denir. b)İkiz Kenar Üçgen:Üçgenin kenarlarının iki tanesi eşit olan üçgene “İkiz Kenar Üçgen” denir. Bir ikizkenar üçgenin, taban açıların ölçüleri birbirine eşittir. c)Eşkenar Üçgen:Üçgenin kenarlarının hepsi eşit olan üçgene “Eşkenar Üçgen” denir. Bir eşkenar üçgenin iç açıları 60º `dir. 2.Açılarına Göre Üçgenler a)Dar Açılı Üçgen:Üçgenin açılarından her birinin ölçüsü 90º`den küçük olan üçgene “Dar Açılı Üçgen” denir. b)Geniş Açılı Üçgen:Bir açısı geniş açı olan üçgene “Geniş Açılı Üçgen” denir. c)Dik Açılı Üçgen:Açılarından birisi dik açı olan üçgene “Dik Açılı Üçgen” denir. Üçgenin Alanını ve Çevresini Bulma Üçgenin çevresini bulabilmek için kenarlar toplanır. Ç = a + b + c Üçgenin alanını bulmak için yükseklikle kenar çarpılır ve ikiye bölünür.  h x a h x b h x c A= --------- = --------- = -------- 2 2 2 ÖZEL ÜÇGENLER (7; 24; 25) dik üçgeni (7; 24; 25) dik üçgeni Dik üçgenlerin dik kenarları 7 ve 24 ile orantılı ise hipotenüs 25 ile orantılıdır.  (45°; 45°; 90°) üçgeni (45°; 45°; 90°) üçgeni Bu üçgen ikizkenar dik üçgendir. Dik kenarlar birbirine eşittir. Hipotenüsün uzunluğu dik kenarların uzunluğunun2 katıdır.  (30°; 60°; 90°) üçgeni (30°; 60°; 90°) üçgeni Eşkenar üçgenin yarısı olan bu üçgende, 30° nin karşısındaki kenarın uzunluğu hipotenüs uzunluğunun yarısı ve 60° nin karşısındaki kenarın uzunluğu 30° nin karşısındaki kenarın uzunluğunun 3 katıdır.  İkizkenar üçgende tepe noktasından çizilen yükseklik hem kenarortay hemde açıortaydır.  ÜÇGENLERDE KENAR - (İÇİ VE UZUNLUK BAĞINTILARI 1. Bir üçgenin bir kenarının uzunluğu, diğer iki kenarın toplamından küçük, farklarının mutlak değerinden büyüktür.  3.Bir üçgende büyük açı karşısında, büyük ke- nar bulunur. m(A) > m(B) > m(C) ise a > b > c dir. 4.Bir üçgenin yükseklik, açıortay ve kenarortayı arasında ha < nA < Va sıralaması vardır. 5.Bir üçgenin çevresi Ç = a + b + c dir. u _ Ç(ABC) 2 u = a + b + c dir. 2 6.Bir ABC de: ha + hj-, + hc < 2u nA + nB + nC * ^u Va + Vb + Vc <2u dır. 8. Menelaus Teoremi: D, E, F noktaları doğrusal ise,  9. Seva Teoremi: [AD], [BE] ve [CF] doğru parçalarının kesim noktası K ise;  11. Bir üçgende iki kenarın orta noktaları birleştirildiğinde elde edilen doğru parçası üçüncü kenara paralel ve uzunluğu üçüncü kenarın yarısı kadardır.   Şekilde verilenlere göre x'in en büyük tam sayı değeri kaçtır? A) 3 B)4 C)6 D) 7 E) 8 Şekilde verilenlere göre oranı kaçtır? Çözüm: ABC'de üçgen eşitsizliğinden; 6-5<3x-1 <6 + 5 1 <3x-1 < 11 2<3x<12 -§-<x<4...(1) ADC'de üçgen eşitsizliğinden; 6-5<3x-2<6 + 5 1 < 3x-2 < 11 3 < 3x < 13 = 1 dir. Açıortay: Üçgende bir açıyı iki eş parçaya bölen doğru parçasına ‘açıortay’ denir.  Üçgenin içaçıortayları üçgen içinde bir noktada kesişir.Bu noktaya ‘içaçıortayların kesim noktası’ denir. İçaçıortayların kesim noktası aynı zamanda üçgenin içteğet çemberinin merkezidir. Kenarortay: Üçgenin bir köşesinden karşı kenarın orta noktasına çizilen doğru parçasına ‘kenarortay’ denir.  Üçgenin kenarortayları üçgen içinde bir noktada kesişirler.Bu nokta üçgenin ‘ağırlık merkezidir’. Şekilde G noktası ABC üçgeninin ağırlık merkezidir. Yükseklik: Üçgende bir köşeden karşı kenara veya karşı kenarın uzantısına dik olarak çizilen doğru parçasına ‘yükseklik’ denir.  Üçgende yükseklikler; ha, hb , hc ile gösterilir. Yükseklikler; üçgenin içinde, üzerinde veya üçgenin dışında bir noktada kesişirler. Bu noktaya üçgenin ‘diklik merkezi’ denir. 1. Benzer Üçgenler Karşılıklı açıları eş ve karşılıklı kenarları orantılı olan üçgenlere benzer üçgenler denir.  ABC ve DEF üçgenleri için;  oranı yazılır Buradan ABC üçgeni ile DEF üçgeni benzerdir denir ve ABC ~ DEF biçiminde gösterilir.  eşitliğinde verilen k sayısına, benzerlik oranı yada benzerlik katsayısı denir. eşitliğinde verilen k sayısına, benzerlik oranı yada benzerlik katsayısı denir.
ABC ~ DEF benzerliği yazılırken eş açıların sıralanmasına dikkat edilir.  2. Açı - Açı Benzerlik Teoremi Karşılıklı ikişer açıları eş olan üçgenler benzerdir.  şekilde verilen üçgenlerde  İkişer açıları eş olduğundan, üçüncü açıları da eş olmak zorundadır. Dolayısıyla bu iki üçgen benzer üçgenlerdir. m(C)=m(F)  3. Kenar - Açı - Kenar Benzerlik Teoremi İki üçgenin karşılıklı ikişer kenarı orantılı ve bu kenarların oluşturduğu karşılıklı açılar eş ise, üçgenler benzerdir.   ABC üçgeni ile DEF üçgeninin BAC ve EDF açıları eş, bu açıların kenarları da orantılı ise, bu iki üçgen benzerdir. BAC açısının kısa kenarının EDF açısının kısa kenarına oranı, BAC açısının uzun kenarının EDF açısının uzun kenarına oranına eşittir. 4. Kenar - Kenar - Kenar Benzerlik Teoremi İki üçgenin karşılıklı bütün kenarları orantılı ise bu iki üçgen benzerdir.   Kenarları orantılı olan ABC ve DEF benzer üçgenlerinde orantılı kenarları gören açılar eştir. m(A) = m(D), m(B) = m(E), m(C) = m(F) 5. Temel Benzerlik Teoremi ABC üçgeninde [DE] // [BC] ise yöndeş açılar eş olacağından ADE ~ ABC dir.   
 6. Tales Teoremi Paralel doğrular kendilerini kesen doğruları aynı oranda bölerler. d1 // d2 // d3 doğruları için  Buradan  de elde edilir de elde edilir
 7. Benzerlik Özellikleri Benzer üçgenlerin açıları karşılıklı olarak eş, diğer bütün elemanları orantılıdır.  ABC ~ DEF Û  Burada k ya benzerlik oranı denir. a. Benzer üçgenlerde orantılı kenarlara ait yüksekliklerin oranı benzerlik oranına eşittir. <B> </B> b. Benzer üçgenlerde orantılı kenarlara ait kenar-ortay uzunluklarının oranı benzerlik oranına eşittir. <B> </B> c. Benzer üçgenlerde eş açılara ait açıortay uzunluklarının oranı benzerlik oranına eşittir. <B> </B> d. Benzer üçgenlerin çevrelerinin oranı benzerlik oranına eşittir. <B> </B> <B>e. ABC üçgeninde içteğet çemberin yarıçapı rABC ve çevrel çemberin yarıçapı RABC , DEF üçgeninde içteğet çemberin yarıçapı rDEF ve çevrel çemberin yarıçapı RDEF olsun. </B> f. Alanlar oranı Benzer üçgenlerin alanlarının oranı benzerlik oranının karesine eşittir.   g. Benzerlik oranı k = 1 olan üçgenler eş üçgenlerdir. <B>

</B>
 8. Özel Teoremler a. Menelaüs ABC üçgeni KM doğru parçası ile şekildeki gibi kesiliyor ise   [b]b. Seva ABC üçgeni içerisinde alınan bir P noktası için,   alıntı |
 |
| | Mesaj No:3 |
| Durumu: Medine No : 13301 Üyelik T.:
04 Şubat 2011 | ÜÇGENLERDE KENAR - (İÇİ VE UZUNLUK BAĞINTILARI 1. Bir üçgenin bir kenarının uzunluğu, diğer iki kenarın toplamından küçük, farklarının mutlak değerinden büyüktür.  3.Bir üçgende büyük açı karşısında, büyük ke- nar bulunur. m(A) > m(B) > m(C) ise a > b > c dir. 4.Bir üçgenin yükseklik, açıortay ve kenarortayı arasında ha < nA < Va sıralaması vardır. 5.Bir üçgenin çevresi Ç = a + b + c dir. u _ Ç(ABC) 2 u = a + b + c dir. 2 6.Bir ABC de: ha + hj-, + hc < 2u nA + nB + nC * ^u Va + Vb + Vc <2u dır. 8. Menelaus Teoremi: D, E, F noktaları doğrusal ise,  9. Seva Teoremi: [AD], [BE] ve [CF] doğru parçalarının kesim noktası K ise;  11. Bir üçgende iki kenarın orta noktaları birleştirildiğinde elde edilen doğru parçası üçüncü kenara paralel ve uzunluğu üçüncü kenarın yarısı kadardır.   Şekilde verilenlere göre x'in en büyük tam sayı değeri kaçtır? A) 3 B)4 C)6 D) 7 E) 8 Şekilde verilenlere göre oranı kaçtır? Çözüm: ABC'de üçgen eşitsizliğinden; 6-5<3x-1 <6 + 5 1 <3x-1 < 11 2<3x<12 -§-<x<4...(1) ADC'de üçgen eşitsizliğinden; 6-5<3x-2<6 + 5 1 < 3x-2 < 11 3 < 3x < 13 = 1 dir.                                     alıntı |
 |
| | Mesaj No:4 |
| Durumu: Medine No : 13301 Üyelik T.:
04 Şubat 2011 | TEMEL TANIMLAR : Çember : Düzlemde (R2) sabit bir noktadan eşit uzaklıkta bulunan noktaların kümesi (Geometrik yeri)dir. 1. Çember bir noktalar kümesidir. 2. Çemberin iç bölgesi (Dairesel kısım) konvextir. 3. Çember ve çemberin dış bölgeleri konvex değildir. 4. Çember içinde bulunduğu düzlemi iki ayrık bölgeye ayırır. Düzlemde Bir Nokta ya da Doğrunun Çembere Göre Durumu : Düzlemde bir doğru ya da doğrunun elemanı olan herhangi bir nokta çembere göre üç temel durumda yer alır.  Çemberin Yardımcı Elemanları : A) Kesen : Bir çemberi farklı iki noktada kesen AB veya d doğrusuna çemberin keseni denir.  B) Kiriş : Çemberin üzerindeki iki farklı noktayı birleştiren doğru parçasıdır. ([AB] kirişi vb.)  Kiriş Özellikleri : 1. Merkezden kirişe indirilen dikme kirişi ve yayını ortalar.   2. Merkezden eşit uzaklıkta olan kirişler ve yayları eşittir.  3. Kirişler merkeze yaklaştıkça uzunlukları artar. En uzun kiriş ÇAP'tır.  4. Paralel iki kirişin arasında kalan yaylar eşittir.   5. Çember içindeki bir noktadan geçen en kısa kiriş o noktada çapa dik olandır. [OP] ^ [AB] ^ [OP] [CD] Û |AB| < |CD|   C) Yay : Çember üzerindeki iki farklı noktanın arasında kalan tüm noktalar kümesidir. D) Teğet : Bir doğrunun çembere bir noktada değmesi halidir.  Teğet Özellikleri : 1. Yarıçap teğete değme noktasında diktir. 2. Bir çembere dışındaki bir noktadan en çok iki teğet çizilir ve teğet parçalarının uzunlukları eşittir.  Teğetler Dörtgeni : Karşılıklı kenarlarının uzunlukları toplamı eşittir. (Kare, eşkenar dörtgen ve deltoid teğetler dörtgenidir.) |AB| + |DC| = |AD| + |BC| = u Alan (ABCD) = u . r  alıntı |
 |
| | Mesaj No:5 |
| Durumu: Medine No : 13301 Üyelik T.:
04 Şubat 2011 | İki Çemberin Birbirine Göre Durumları : a) Ayrık :   b) Dıştan Teğet   c) Kesişme Hali  d) İçten Teğet  e) Alt Küme (İç içe) Hali  f) Dik Kesişen Çemberler. Kesişme noktaları olan K ve K' nden ve merkezlerinden geçen teğetler birbirine dik ise iki çember dik kesişirler.   İki Çemberin Ortak Teğetleri a) Ortak Dış Teğet Parçasının Uzunluğu (d)   b) Ortak İç Teğet Parçasının Uzunluğu (d)   Üçgenin Çemberleri 1. İç Teğet Çember : (İçaçıortayların kesim noktasıdır.) İspat :  |AD| = (u-a) |AF| = |AD| = x diyelim. |BD|=|BE|=(c-x) |CF|=|CE|=(b-x) |BC|=a=(c-x)+(b-x) 2x=b+c-a (sağ tarafa a ekleyip a çıkartalım) 2x=a+b+c-2a  x=u-a |AD| = |AF| = (u-a) |BD| = |BE| = (u-b) |CE| = |CF| = (u-c) İspat : "Açıortay üzerinde alınan bir noktanın (O) açının kollarına olan uzaklıkları eşittir." teoremini kullanarak |OF| = |OE| = |OD| elde edilir. Düzlemde bir noktadan eşit uzaklıkta bulunan (O noktasından r uzaklıkta bulunan D, E, F noktaları) en az üç nokta bir çember belirler özelliği de bize ABC üçgeninin içteğet çemberinin O merkezli r yarıçaplı çember olduğunu ispatlar. 2. Dış Teğet Çember : (İki dış açıortay ve üçüncü açının iç açıortayının kesim noktasıdır.) Dışteğet çemberlerin yarıçapları  ve içteğet çemberin yarıçapı r ise; ve içteğet çemberin yarıçapı r ise;  bağıntısı vardır. |AE| = |AF| = u |AB| = c |AC| = b |BC| = a |BD| = |BE| = (u-c) |CD| = |CF| = (u-b)  İspat : |BE| = |BD| = (u-c) = x |CF| = |CD| = (u - b) = y alalım. x+y =a dır. c+x = b+y = |AE| = |AF| dir. her iki tarafa y ekleyelim. c + x + y = b + 2y Şc + a - b = 2y (Sol tarafa "b" ekleyip çıkaralım.) a + b + c - 2b = 2y  y=(u-b) 3. Çevrel Çember : (Merkezi; üçgenin kenarorta dikmelerin kesim noktasıdır. Yarıçapı R dir.) Bu özelliğin ispatını "Merkezden kirişe indirilen dikme kirişi ve yayını ortalar." teoremiyle yapabilirsiniz.  Kural : BAC açısının açıortayı olan [AD] ile [BC] kenarının kenar orta dikmesi olan [OD], D noktasında kesişir. İspat : "Merkezden kirişe indirilen dikme kirişi ve yayını ortalar ve Aynı yayı gören çevre açılar (BAD) ve (CAD) eşittir." kuralını hatırlayınız.  Kural :  İspat :  alıntı |
 |
| | Mesaj No:6 |
| Durumu: Medine No : 13301 Üyelik T.:
04 Şubat 2011 | Çemberde Açılar : 1. Merkez Açı : Köşesi çemberin merkezinde bulunan açıdır. Ölçüsü gördüğü yayın ölçüsüne eşittir.   2. Çevre Açı : Köşesi çember üzerinde olan ve kolları çemberi kesen açıdır. Ölçüsü gördüğü yayın ölçüsünün yarısıdır. Aynı yayı gören çevre açılar eşittir.   İspat : [AO ışını ile açısını iki parçaya ayıralım. merkez açısının gördüğü yayı gören çevre açısı onun yarısı olur.  Kural : Çapı gören çevre açı 90° dir.  3. Teğet-Kiriş Açı : Köşesi çember üzerinde olup, bir kolu çemberin o noktadaki teğeti, diğer kolu o noktadan geçen kirişi olan açıdır. Ölçüsü gördüğü yayın ölçüsünün yarısıdır.   İspat : [OA] yarıçap çizilirse;   4. İç Açı : Çemberin iç bölgesinde kesişen iki kiriş arası açıdır. Ölçüsü gördüğü yayların ölçüleri toplamının yarısıdır.   İspat : A ve C noktalarını birleştirelim. m ve n çevre açıları CyD ve AxB yaylarını görür. AEC üçgeninde "iki iç açı eşittir, bir dış açı" kuralından ;   5. Dış Açı : Ölçüsü gördüğü yayların ölçüleri farkının yarısıdır.   İspat :   Kural :   Kural : Aynı yayları gören iç ve dış açıların toplamı gördükleri büyük yayın ölçüsüne eşittir. Aynı yayları gören iç ve dış açıların farkı gördükleri küçük yayın ölçüsüne eşittir.   Kirişler Dörtgeni :  Karşılıklı açılarının toplamı eşittir. (180°) - Kare, dikdörtgen, ikizkenar yamuk kirişler dörtgenidirler. - e ve f dörtgenin köşegenleri ise;   a.c + b.d = e.f bağıntısı vardır. ise; Noktanın Çembere Göre Kuvveti : 1. Çemberdışı bir noktanın kuvveti :  Kuvvet = |PT|  = |PA| . |PB| = |PC| . |PD| = |PA| . |PB| = |PC| . |PD| - Kuvvet vektörel bir nicelik olarak alınırsa, çember dışı bir noktanın kuvveti pozitiftir. İspat :  PTO dik üçgeninden Kuvvet = |PT|  = |PO| = |PO| -r -r > 0 > 0 İspat : ABDC kirişler dörtgeninde karşılıklı açılar bütünlerdir.   2. Çember üzeri bir noktanın kuvveti O dır. 3. Çember içindeki bir noktanın kuvveti |PA| . |PB| = |PC| . |PD| - Kuvvet vektörel bir nicelik olarak alınırsa çember içi bir noktanın kuvveti negatiftir.  İspat : Kuvvet = |PO|  - r - r idi idi (Kuvvet : Nokta merkez arası uzaklığın karesinden yarıçapın karesi çıkarılarak bulunur.) POD dik üçgeninden, Kuvvet = |PD|  = |PO| = |PO| - r - r < 0 < 0 |PD| = |PC| olduğundan; Kuvvet = |PD| . |PC| = |PA| . |PB| = |PD|  - r - r < 0 < 0  İspat : Çevre açıları eşliğinden;   İki Çemberin Kuvvet Ekseni : İki çembere göre aynı kuvvette olan noktaların kümesi olan doğruya denir. Çemberlerin merkezlerini birleştiren doğruya diktir. a)  b) |PT|  = |PT'| = |PT'| = |PA| . |PB| = |PA| . |PB|  c)  |PT|  = |PT'| = |PT'| = |PA| . |PB| = |PC| . |PD| = |PA| . |PB| = |PC| . |PD| d) |PT|  = |PA| . |PB| = |PC| . |PD| = |PA| . |PB| = |PC| . |PD|  Üç Çemberin Kuvvet Merkezi : Üç çemberin ikişer ikişer kuvvet eksenlerinin kesim noktasıdır.      Daire Dilimi (Kesmesi) Alanı :    Daire Parçası Alanı :   Daire Halkası Alanı :   Halka Dilimi Alanı :   alıntı |
 |
| | Mesaj No:7 |
| Durumu: Medine No : 13301 Üyelik T.:
04 Şubat 2011 | Yamuk Konu Özeti İki kenarı birbirine paralel olan dörtgene yamuk denir. Paralel olan kenarlar yamuğun tabanları diğer iki kenarlarına da yan kenarları denir. (Şek.27) *Bir yamukta yan kenarlardan birine bitişik açılar birbirlerini bütünler. m(A) + m(D) = m(B) + m(C) = 1800 *Yamuğun çevresi Ç= a+b+c+d Yamuğun alanı A=  alıntı |
 |
| | Mesaj No:8 |
| Durumu: Medine No : 13301 Üyelik T.:
04 Şubat 2011 | GEOMETRİK CİSİMLER NELERDİR?  PİRAMİT: Piramidin temel elemanları tepe noktası, tabanı, yan yüzleri, ayrıtları ve yüksekliğidir. Piramidin tepe noktasından taban düzlemine inen dikme veya bu dikmenin uzunluğu piramidin yüksekliğidir. Tepe noktasını taban merkezine (ağırlık merkezine) birleştiren doğru parçası tabana dik ise piramide dik piramit, eğik ise eğik piramit denir. Piramitler, tabanlarını oluşturan çokgensel bölgelere göre üçgen dik pirami, kare eğik piramit vb. şeklinde adlandırılır. Dik piramitlerin yüzey alanı, taban alanı ile yan yüzlerini oluşturan üçgensel bölgelerin alanları toplanarak bulunur. Bir dik piramidin hacmi, tabanı ve yüksekliği piramidin tabanı ve yüksekliğine eş olan dik prizmanın hacminin üçte birine eşittir.   KONİ: Koninin temel elmanları; bir daire olan taban, tabanın dışında bir tepe noktası, tepe noktasını taban merkezine birleştiren doğru parçası olan eksen, tepe noktasından geçen ve tabanın çevresini oluşturan çembere dayanan bir doğrunun süpürdüğü yanal yüzey, bu doğrudan ibaret olan ana doğru (doğuran) 'dur. Ekseni tabana dik olan koni dik koni (veya dönel koni), eğik olan koni eğik koni olarak adlandırılır. Dik koninin yanal yüzü, bir dairenin belirli bir merkez açısıyla elde edilen sektörüdür. Koninin tabanı, çevresini uzunluğu bu sektörün yay uzunluğuna eşit olan dairedir. Dik dairesel koninin yüzey alanı, koninin yanal yüzey alanı ile taban alanı toplanarak bulunur. Sektörün alanı demek daire diliminin alanı demektir. Bir dönel koninin düzlemlerle arakesitine, konikler adı verilir. Herhangi bir koni, tabana paralel bir düzlemle kesilirse, düzlemle taban arasında kalan kısma kesik koni denir.    KÜRE: Kürenin temel elemanları; bir merkez noktası, bu merkez noktasından eşit uzaklıkta bulunan noktaların oluşturduğu yüzey ve yüzeyin herhangi bir noktasını merkeze birleştiren doğru parçası (yarıçap) 'dır. Özel bir küre, merkezi ve yarıçapı dikkate alınarak hesaplanır. Merkezden geçen düzlemlerle kürenin ara kesiti olan dairenin çapı aynı zamanda kürenin çapıdır. Merkezinden geçen düzlemlerle küre yüzeyinin ara kesitine büyük çemberler adı verilir. Kürenin büyük dairesi, kürenin merkezini içine alan veya merkezinden geçen dairedir. Kürenin yüzey alanı, kürenin en büyük dairesinin alanının 4 katına eşittir. En büyük çemberin yarıçap uzunluğu r olan bir kürenin hacmi, taban yarıçapı r ve yüksekliği 2r olan dik silindirin hacminin 2/3 üne eşittir.    Formüller (İki boyutlu, standart) bir küre için kimi formüller: Küre formülleri Hacim  Projeksiyon Alanı 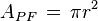 Küre parçasının hacmi  Yarıçap  Yükseklik  Atalet momenti  SİLİNDİR: Silindir geometrik bir cisimdir.
Bir dikdörtgenin bir kenarı etrâfında döndürülmesiyle elde edilir. Bu silindire dik veya eğik silindir denir. Alt ve üst tabanı dâiredir. Soba borusu dik silindire bir örnektir. Matematikte silindirin genel tanımı şöyledir: Düzlemsel bir eğriyle bu eğrinin düzleminde bulunmayan bir doğru verildiğinde, dâimâ bu doğruya paralel kalmak şartıyla eğriye dayanarak hareket eden bir doğrunun taradığı yüzeye silindirik yüzey denir. Bu silindirik yüzeyle, bu yüzeyi kesen paralel iki düzlemin sınırladığı cisme silindir denir. Silindir yüzeyini meydana getiren doğrulardan herbirine ana doğru denir. Silindire, taban eğrisine göre isim verilir. Eğri dâireye Şişe dâirevî silindir, elipse ise eliptik silindir denir. Silindirik yüzey için taban eğrisinin kapalı olması gerekmez. Parabolik silindir, hiperbolik silindir, birer silindirik yüzeydir. Dairevî silindirin ana doğrusu tabana dik değilse böyle silindire eğik silindir denir. Taban yarıçapı “r”, yüksekliği “h” olan bir dik silindirin alan ve hacim formülleri şöyledir: Yan alan: Y=2πrh İki taban alanı: 2A=2πr2 Bütün alanı: S=Y+2A=2πrh+2πr2=2πr (h+r) Hacmi: V= π r2. h Bayındırlıkta: Bir şasiye monte edilmiş, tekerlek vazîfesi gören bir veya birkaç büyük mâdenî silindirden meydana gelen ve toprağı, şaseleri kaplayan malzemeyi sıkıştırmak ve ezmek için kullanılan, dökme demirden yapılmış büyük ağırlığa, şeklinden dolayı silindir adı verilir. Otomobilde, tekstil ve kâğıt sanâyiinde çeşitli silindirler kullanılmaktadır.   alıntı |
 |
| | Mesaj No:9 |
| Durumu: Medine No : 13301 Üyelik T.:
04 Şubat 2011 |
Bir düzlemde kapalı bir bölge ile bu düzlemin dışında bir T noktası alalım. Kapalı bölgenin tüm noktalarının T noktası ile birleştirilmesi sonucunda oluşan cisme piramit denir.  T noktası piramidin tepe noktasıdır. Kapalı bölge ise piramidin tabanıdır. Piramit; tabanı oluşturan şeklin ismiyle adlandırılır. Taban kare ise, kare piramit; taban altıgense altıgen piramit gibi. Eğer piramidin tabanı düzgün çokgense bu tip piramitlere düzgün piramit denir. T noktasının taban düzlemi üzerindeki dik izdüşümüne H dersek [TH] piramidin yüksekliği olur. |TH| = h biçiminde yazılır. [TA], [TB], [TC]� piramidin yanal ayrıtlarıdır. Piramitlerin hacmi taban alanı ile yüksekliğin çarpımının üçte biri kadardır.  1.Kare Piramit Kare piramidin tabanı kare biçimindedir. Yan yüzeyleri ise dört adet ikizkenar üçgenden oluşur. İkizkenar üçgenlerin taban uzunlukları piramidin tabanının bir kenarına eşittir. |PH| = h piramidin yüksekliğidir. Yan yüz yüksekliği |PK| dır. Tabanının bir kenarına a dersek  Buradan yan yüz yüksekliği |PK|2 = h2 + (  )2 olur. )2 olur.  Tüm alan yan yüz alanları ile taban alanının toplamına eşittir. 2. Eşkenar Üçgen Piramit Tabanı eşkenar üçgen olan piramitlere eşkenar üçgen piramit denir.  Taban Alanı  olduğundan  3. Düzgün Dörtyüzlü  Dört yüzü de eşkenar üçgenlerden oluşan cisimdir. Yükseklik, tabanı oluşturan üçgenin ağırlık merkezine iner. Bir ayrıtı a olan düzgün dörtyüzlünün Yarı yüz yüksekliği  ve Cisim yüksekliği  olur Buradan   4. Düzgün Sekizyüzlü Bütün ayrıtları birbirine eş ve yüzeyleri sekiz eşkenar üçgenden oluşan cisme düzgün sekizyüzlü denir. Bir ayrıtına a dersek yan yüz yüksekliği  olur. olur.Cismin, ortak tabanlı iki adet kare piramitten oluştuğunu düşünürsek piramitlerin yüksekliği; olur.  Piramitin hacmi  olduğundan; olduğundan;  Yüzey şekilleri eşkenar üçgen olduğundan  5. Düzgün Altıgen Piramit Tabanı düzgün altıgen olan piramide düzgün altıgen piramit denir. Yan yüzeyleri altı adet eş ikizkenar üçgenden oluşur. KONİ Tabanı daire biçiminde olan piramide koni adı verilir. Taban alanı =  olduğundan   bulunur. Yan yüzeyleri altı adet eş ikizkenar üçgen oluşur. KONİ  Tabanı daire biçiminde olan piramite koni adı verilir. Burada; Taban yarıçapı |OB| = r Cisim yüksekliği |PO| = h olur. |PA| = |PB| = l uzunluğuna ana doğru denir. POB dik üçgeninde, h2 + r2 = l2 bağıntısı vardır. Koninin yanal alanı bir daire dilimidir.  Daire diliminin alanı, yay uzunluğu ile yarıçapın çarpımının yarısıdır. Yay uzunluğu taban çevresine eşit olduğundan, Yanal alan= pr2+prl Tüm alan bulunurken, taban alanı da ilave edilir. Tüm alan = �r2 + �rl
 oranı elde ederiz.

  Kesik piramitlerin hacimleri bulunurken cisim piramide tamamlanır. [O1B] // [O2D] olduğundan  benzerliği vardır. Küçük koninin büyük koniye benzerlik oranı  dir. Alanları dir. Alanlarıoranı benzerlik oranının karesi olduğundan, alanlar oranı  olur. Hacimler oranı olur. Hacimler oranıise benzerlik oranının küpüdür. r1 yarıçaplı küçük koninin hacmine V1, r2 yarıçaplı büyük koninin hacmine V2 dersek   alıntı |
 |
| | Mesaj No:10 |
| Durumu: Medine No : 13301 Üyelik T.:
04 Şubat 2011 |
Alt ve üst tabanları paralel eş şekillerden oluşan cisimlere prizma denir. Yan yüzeyleri taban düzlemine dik olan prizmalara dik prizma adı verilir. [] Prizmalarda yan yüzeyleri birleştiren ayrıtlara yanal ayrıt denir. [AA'], [BB'], [CC'], [DD'] yanal ayrıtlardır. Dik prizmalarda yanal ayrıt cismin yüksekliğine eşittir. Cismin yüksekliğine h dersek h = |AA'| = |BB'| = |CC'| = |DD'| olur. [ Prizmanın Hacmi Hacim=Taban Alanı x Yükseklik [ Dik prizmanın taban biçimi nasıl olursa olsun, yanal yüzeyi daima bir dikdörtgen olur. Yanal yüzü oluşturan dikdörtgenin alt kenarı tabanın çevresi kadardır. Diğer kenarı ise h yüksekliği kadar olur. Yanal Alan = Taban çevresi x Yükseklik Bütün dik prizmaların yanal alanı taban çevresi ile yüksekliğin çarpımıdır. Bütün Alan ise yanal alan ile iki taban alanının toplamıdır. Tüm Alan = Yanal Alan + 2. Taban Alanı 1. Dikdörtgenler Prizması Dikdörtgenler prizması yan yüzeyleri karşılıklı ikişer ikişer eş olan altı adet dikdörtgenden oluşan prizmadır. Burada hacim, taban alanı olan (a.b) ile yükseklik olan (c) nin çarpımıdır. Alan ise (a.b), (b.c) ve (a.c) yüzey alanlarının ikişer katlarının toplamıdır. Dikdörtgenler prizmasında birbirine en uzak iki köşeyi birleştiren doğru parçasına cisim köşegeni denir. [ Cisim köşegeni daima prizmanın içinden geçer. Yüzeylerinden geçmez. Sadece bir yüzeyden geçen köşegene o yüze ait yüzey köşegeni denir. Burada köşegenlerin uzunlukları |AC'| = |A'C| = |BD'| = |B'D| = e (cisim köşegeni) |BD| = f (Yüzey köşegeni) olsun. Bu durumda Hacim = a.b.c Alan =2(ab+bc+ac) Alan = 2 (ab + bc + ac) Cisim Köşegeni: e =Öa2 + b2 + c2 Yüzey Köşegeni: f = Öa2 + b2 2. Kare Prizma Tabanı kare olan prizmalara kare prizma denir. Yan yüzü dört adet eş dikdörtgenden oluşur.  Hacim = a2 . h Yanal Alan = 4 . a . h Alan = 4.ah + 2.a2 Cisim köşegeni : e = Öa2 + a2 + h2 3. Küp Bütün ayrıtları birbirine eşit olan dik prizmaya küp denir. Tüm yüzeyleri kare dir. ] Hacim = a3 Alan = 6a2 Kübün yüzey köşegenleri birbirine eşittir. Yüzey köşegeni: f = aÖ2 Cisim köşegeni: e = aÖ3 4. Üçgen Prizmalar Prizmalar tabanlarının şekline göre isim aldıklarından tabanı üçgen olan prizmalara üçgen prizma denir. Üçgen prizmalar tabanını oluşturan üçgene göre isimlenir. a. Eşkenar Üçgen Prizma Eşkenar üçgen prizmanın tabanları eşkenar üçgendir. Yan yüzeyleri ise üç tane eş dikdörtgenden oluşur.Tabanı eşkenar üçgen olduğundan Tabanı eşkenar üçgen olduğundan Taban alanı [ Hacim Taban çevresi 3a olduğundan, yanal alan 3a.h dır. Buradan tüm alanı Tüm alan [ b. Dik Üçgen Prizma Dik üçgen prizmanın tabanı dik üçgendir. Yan yüzeyleri ise üç tane dikdörtgenden oluşur. [] Tabanı dik üçgen olduğundan Taban alanı =  Hacim  Taban çevresi a + b + c olduğundan, Yanal alan = (a + b + c) . h Tüm Alan = b . c + (a + b + c) . h 5. Silindir Tabanı daire olan prizmalara silindir denir. Silindirin yan yüzü dikdörtgen biçimindedir. Dikdörtgenin bir kenarı yükseklik kadar, diğer kenarı ise taban dairesinin çevresi kadardır. [SIZE=4]/SIZE] Taban alanı= pr2 Hacim= pr2h Taban çevresi 2pr olduğundan yanal alan 2prh olur. Tüm alan = 2prh+ 2pr Bir dikdörtgen levha bir kenarı etrafında döndürüldüğünde silindir elde edilir. 6. Düzgün Çokgen Prizmalar Tabanı düzgün çokgenlerden oluşan prizmalara düzgün çokgen prizmalar deriz. Taban ayrıtları birbirine eşittir. Diğer dik prizmalarda olduğu gibi düzgün çokgen prizmalarda da yanal ayrıt aynı zamanda yüksekliktir.
EĞİK PRİZMALAR 1. Eğik Kare Prizma Tabanı, bir kenarı a olan kareden oluşan prizma bir yöne doğru taban düzlemi ile a açısı yapacak kadar eğilirse eğik kare prizma elde edilir. Prizmanın yanal ayrıtlarına l dersek, Prizmanın yüksekliği h =l .sin a olur. Eğik prizmanın yanal ayrıtlarına dik olacak şekilde oluşan kesitine dik kesit denir. Eğik kare prizmanın iki yan yüzeyi dikdörtgen, diğer iki yan yüzeyi ise paralelkenardır. Eğik kare prizmanın dik kesitinin bir kenarı taban kenarı a kadar, diğeri ise, a'=a.sin a kadardır. Buradan; Dik Kesit Alanı = Taban Alanı x Sin a Dik kesit çevresi = 2a +2a.sin a Eğik prizmaların yanal alanlarının toplamı Yanal alan= Dik kesit çevresi x Yanal Ayrıt bağıntısı ile bulunur. Alt ve üst tabanlar ilave edildiğinde tüm alan bulunmuş olur. Bütün prizmalarda olduğu gibi eğik prizmalarda da hacim, taban alanı ile yüksekliğin çarpımı ile bulunur. Hacim = Taban Alanı x Yükseklik Ayrıca dik kesit alanı ile yanal ayrıtın çarpımı ile de hacim bulunabilir. Hacim = Dik Kesit Alanı x Yanal Ayrıt 2. Eğik Silindir |AA'| = |BB'| = l Yanal ayrıtı l olan ve taban düzlemi ile a açısı yapan eğik silindirde yükseklik, h=l.sin a Dik Kesit Alanı=Taban Alanı x Sin a ] Eğik silindirin yan yüz alanı, dik kesit çevresi ile yanal ayrıtının çarpımıdır. Bütün eğik prizmalarda olduğu gibi eğik silindir de de hacim, dik kesit alanı ile yanal ayrıtın çarpımına eşittir. Hacim = Taban Alanı x Yükseklik Hacim = Dik Kesit Alanı x Yanal Ayrıt Yanal Alan = Dik Kesit Çevresi x Yanal Ayrıt
Alt ve üst tabanları paralel eş şekillerden oluşan cisimlere prizma denir. Yan yüzeyleri taban düzlemine dik olan prizmalara dik prizma adı verilir. Prizmalarda yan yüzeyleri birleştiren ayrıtlara yanal ayrıt denir. [AA'], [BB'], [CC'], [DD'] yanal ayrıtlardır. Dik prizmalarda yanal ayrıt cismin yüksekliğine eşittir. Cismin yüksekliğine h dersek h = |AA'| = |BB'| = |CC'| = |DD'| olur. Prizmanın Hacmi Hacim=Taban Alanı x Yükseklik Dik prizmanın taban biçimi nasıl olursa olsun, yanal yüzeyi daima bir dikdörtgen olur. Yanal yüzü oluşturan dikdörtgenin alt kenarı tabanın çevresi kadardır. Diğer kenarı ise h yüksekliği kadar olur. Yanal Alan = Taban çevresi x Yükseklik Bütün dik prizmaların yanal alanı taban çevresi ile yüksekliğin çarpımıdır. Bütün Alan ise yanal alan ile iki taban alanının toplamıdır. Tüm Alan = Yanal Alan + 2. Taban Alanı 1. Dikdörtgenler Prizması Dikdörtgenler prizması yan yüzeyleri karşılıklı ikişer ikişer eş olan altı adet dikdörtgenden oluşan prizmadır. Burada hacim, taban alanı olan (a.b) ile yükseklik olan (c) nin çarpımıdır. Alan ise (a.b), (b.c) ve (a.c) yüzey alanlarının ikişer katlarının toplamıdır. Dikdörtgenler prizmasında birbirine en uzak iki köşeyi birleştiren doğru parçasına cisim köşegeni denir. Cisim köşegeni daima prizmanın içinden geçer. Yüzeylerinden geçmez. Sadece bir yüzeyden geçen köşegene o yüze ait yüzey köşegeni denir. Burada köşegenlerin uzunlukları |AC'| = |A'C| = |BD'| = |B'D| = e (cisim köşegeni) |BD| = f (Yüzey köşegeni) olsun. Bu durumda Hacim = a.b.c Alan =2(ab+bc+ac) Alan = 2 (ab + bc + ac) Cisim Köşegeni: e =Öa2 + b2 + c2 Yüzey Köşegeni: f = Öa2 + b2 2. Kare Prizma Tabanı kare olan prizmalara kare prizma denir. Yan yüzü dört adet eş dikdörtgenden oluşur.  Hacim = a2 . h Yanal Alan = 4 . a . h Alan = 4.ah + 2.a2 Cisim köşegeni : e = Öa2 + a2 + h2 3. Küp Bütün ayrıtları birbirine eşit olan dik prizmaya küp denir. Tüm yüzeyleri kare dir. ] Hacim = a3 Alan = 6a2 Kübün yüzey köşegenleri birbirine eşittir. Yüzey köşegeni: f = aÖ2 Cisim köşegeni: e = aÖ3 4. Üçgen Prizmalar Prizmalar tabanlarının şekline göre isim aldıklarından tabanı üçgen olan prizmalara üçgen prizma denir. Üçgen prizmalar tabanını oluşturan üçgene göre isimlenir. a. Eşkenar Üçgen Prizma Eşkenar üçgen prizmanın tabanları eşkenar üçgendir. Yan yüzeyleri ise üç tane eş dikdörtgenden oluşur.Tabanı eşkenar üçgen olduğundan [] Tabanı eşkenar üçgen olduğundan Taban alanı Hacim Taban çevresi 3a olduğundan, yanal alan 3a.h dır. Buradan tüm alanı Tüm alan b. Dik Üçgen Prizma Dik üçgen prizmanın tabanı dik üçgendir. Yan yüzeyleri ise üç tane dikdörtgenden oluşur. Tabanı dik üçgen olduğundan Taban alanı = Hacim Taban çevresi a + b + c olduğundan, Yanal alan = (a + b + c) . h Tüm Alan = b . c + (a + b + c) . h 5. Silindir Tabanı daire olan prizmalara silindir denir. Silindirin yan yüzü dikdörtgen biçimindedir. Dikdörtgenin bir kenarı yükseklik kadar, diğer kenarı ise taban dairesinin çevresi kadardır. Taban alanı= pr2 Hacim= pr2h Taban çevresi 2pr olduğundan yanal alan 2prh olur. Tüm alan = 2prh+ 2pr Bir dikdörtgen levha bir kenarı etrafında döndürüldüğünde silindir elde edilir. 6. Düzgün Çokgen Prizmalar Tabanı düzgün çokgenlerden oluşan prizmalara düzgün çokgen prizmalar deriz. Taban ayrıtları birbirine eşittir. Diğer dik prizmalarda olduğu gibi düzgün çokgen prizmalarda da yanal ayrıt aynı zamanda yüksekliktir.
EĞİK PRİZMALAR 1. Eğik Kare Prizma Tabanı, bir kenarı a olan kareden oluşan prizma bir yöne doğru taban düzlemi ile a açısı yapacak kadar eğilirse eğik kare prizma elde edilir. Prizmanın yanal ayrıtlarına l dersek, Prizmanın yüksekliği h =l .sin a olur. Eğik prizmanın yanal ayrıtlarına dik olacak şekilde oluşan kesitine dik kesit denir. Eğik kare prizmanın iki yan yüzeyi dikdörtgen, diğer iki yan yüzeyi ise paralelkenardır. Eğik kare prizmanın dik kesitinin bir kenarı taban kenarı a kadar, diğeri ise, a'=a.sin a kadardır. Buradan; Dik Kesit Alanı = Taban Alanı x Sin a Dik kesit çevresi = 2a +2a.sin a Eğik prizmaların yanal alanlarının toplamı Yanal alan= Dik kesit çevresi x Yanal Ayrıt bağıntısı ile bulunur. Alt ve üst tabanlar ilave edildiğinde tüm alan bulunmuş olur. Bütün prizmalarda olduğu gibi eğik prizmalarda da hacim, taban alanı ile yüksekliğin çarpımı ile bulunur. Hacim = Taban Alanı x Yükseklik Ayrıca dik kesit alanı ile yanal ayrıtın çarpımı ile de hacim bulunabilir. Hacim = Dik Kesit Alanı x Yanal Ayrıt 2. Eğik Silindir |AA'| = |BB'| = l Yanal ayrıtı l olan ve taban düzlemi ile a açısı yapan eğik silindirde yükseklik, h=l.sin a Dik Kesit Alanı=Taban Alanı x Sin a Eğik silindirin yan yüz alanı, dik kesit çevresi ile yanal ayrıtının çarpımıdır. Bütün eğik prizmalarda olduğu gibi eğik silindir de de hacim, dik kesit alanı ile yanal ayrıtın çarpımına eşittir. Hacim = Taban Alanı x Yükseklik Hacim = Dik Kesit Alanı x Yanal Ayrıt Yanal Alan = Dik Kesit Çevresi x Yanal Ayrıt alıntı |
 |
 |
| Konuyu Toplam 1 Kişi okuyor. (0 Üye ve 1 Misafir) | |
 Benzer Konular
Benzer Konular | ||||
| Konu Başlıkları | Konuyu Başlatan | Medineweb Ana Kategoriler | Cevaplar | Son Mesajlar |
| KPSS Vatandaşlık Dersi Konu Özetleri | Medineweb | Vatandaşlık | 12 | 30 Ekim 2018 09:55 |
| DGS Türkçe Dersi Konu Özetleri | Medineweb | DGS (Dikey Geçiş Sınavı) | 8 | 21 Mayıs 2017 22:13 |
| DGS Matematik Dersi Konu Özetleri-MEDİNEWEB | Medineweb | DGS (Dikey Geçiş Sınavı) | 41 | 12 Nisan 2014 13:56 |
| kelama giriş dersi konu özetleri | makbergülü | Kelama Giriş | 0 | 17 Şubat 2013 16:01 |
| KPSS Coğrafya Dersi Konu Özetleri | Medineweb | Coğrafya | 35 | 05 Ağustos 2012 22:29 |
| .::.Bir Ayet-Kerime .::. | .::.Bir Hadis-i Şerif .::. | .::.Bir Vecize .::. |
|
|